Question

A box rests on top of a flat bed truck. The box has a mass of m = 16.0 kg. The coefficient of static friction between the box and truck is ?s = 0.87 and the coefficient of kinetic friction between the box and truck is ?k = 0.69.

1) The truck accelerates from rest to vf = 17.0 m/s in t = 13.0 s (which is slow enough that the box will not slide). What is the acceleration of the box?
2) In the previous situation, what is the frictional force the truck exerts on the box?
3) What is the maximum acceleration the truck can have before the box begins to slide?
4) Now the acceleration of the truck remains at that value, and the box begins to slide. What is the acceleration of the box?
5) With the box still on the truck, the truck attains its maximum velocity. As the truck comes to a stop at the next stop light, what is the magnitude of the maximum deceleration the truck can have without the box sliding?

Answer 1

1) 1.31 m/s2

2) 20.92 N

3) 8.53 m/s2

4) 1.76 m/s2

5) -8.53 m/s2

Step-by-step explanation:

1) As the box does not slide, the acceleration of the box (relative to ground) is the same as acceleration of the truck, which goes from 0 to 17m/s in 13 s

`a = (\Delta v)/(\Delta t) = (17 - 0)/(13) = 1.31 m/s2`

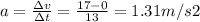
2)According to Newton 2nd law, the static frictional force that acting on the box (so it goes along with the truck), is the product of its mass and acceleration

`F_s = am = 1.31*16 = 20.92 N`

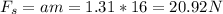
3) Let g = 9.81 m/s2. The maximum static friction that can hold the box is the product of its static coefficient and the normal force.

`F_(\mu_s) = \mu_sN = mg\mu_s = 16*9.81*0.87 = 136.6N`

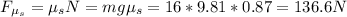
So the maximum acceleration on the block is

`a_(max) = F_(\mu_s) / m = 136.6 / 16 = 8.53 m/s^2`

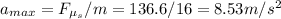
4)As the box slides, it is now subjected to kinetic friction, which is

`F_(\mu_s) = mg\mu_k = 16*9.81*0.69 = 108.3 N`

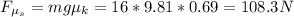
So if the acceleration of the truck it at the point where the box starts to slide, the force that acting on it must be at 136.6 N too. So the horizontal net force would be 136.6 - 108.3 = 28.25N. And the acceleration is

28.25 / 16 = 1.76 m/s2

5) Same as number 3), the maximum deceleration the truck can have without the box sliding is -8.53 m/s2