Question

Steve spends his summers in Florida hanging out with friends at the beach, eating meals of hot dogs and lemonade. The hot dog-lemonade combo costs $5 and Steve's utility from consuming the combos, C, is U(C) = 40C0.5. Given this information, Steve optimizes by consuming ______ meals.

Answer 1

16

Step-by-step explanation:

In economics, total utility (U) is the total satisfaction a consumer derived from consuming a commodity.

Under utility, there is what is called marginal utility (MU). Marginal utility is an extra utility a consumer derives from consuming an extra unit of a good.

Conditions under which consumer optimizes or maximizes his utility for a single good is different for two or more goods.

For one good, a consumer optimizes his utility when the MU of the good is equal price of the good. This can be expressed as follows:

MU(X) = P(X) ..................................... (1)

Equation (1) implies that MU of good X is equal to the price of good X, and the consumer optimizes his utility of good X at that point.

For two or more goods, a consumer optimizes his utility when the MU of all the goods are equal. Given two goods X and Y, for example, utility optimization of a consumer can be expressed as follows:

NU(X) = MU(Y) = ................................ (2)

Equation (2) implies that MU of good X is equal to the MU of good Y, and the consumer optimizes his utility at that point.

From the question, only one good which is hot dog-lemonade combo, C, is being considered. Therefore, the relevant equation to apply is equation (1).

Since total utility from C is given as follows:

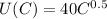`U(C) = 40C^(0.5)` ................................ (3)

MU can be derived by differentiating equation (3) with respect C as follows:

`MU(C) = dU(C)/dC = 0.5(40)C^(0.5-1)`

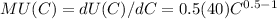
`MU(C) = 20C^(-0.5)` ....................... (4)

Recall that in equation (1), MU(X) = P(X), we follow the same thing and equate MU(C) in equation (4)to the price of C, P(C) as follows:

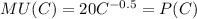`MU(C) = 20C^(-0.5) = P(C)` ....... (5)

Since P(C) is equal to $5 from the question, we can substitute for it in equation (5) and solve for C as follows:

`20C^(-0.5) = $5`

`20(1)/(C^(0.5)) = $5`

`20 = 5C^(0.5)`

`(20)/(5) = C^{(1)/(2) }`

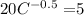
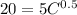
`4 = C^{(1)/(2) }` ............................................. (6)

Squaring both sides of equation (6), we have:

`4^(2) = (C^{(1)/(2) })^(2)`

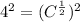
C = 16

Therefore, Steve optimizes by consuming 16 meals

I wish you the best.