Question

A manager wishes to determine the relationship between the number of miles (in hundreds of miles) the manager's sales representatives travel per month and the amount of sales (in thousands of dollars) per month. Find the equation of the regression line for the given data. Predict the value of sales when the sales representative travel 8 miles. Predict the value of sales when tthe sales representative traveled 11 miles.

Miles Traveled, x 2,3,10,7,8,15,3,1,11
Sales, y 31,33,78,62,65,61,48,55,120

Answer 1

a,b,d

Explanation:

because of common sence

UwU

Answer 2

`y=3.529 x +37.91`

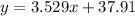
We can predict the sales representative travelled 8 miles replacing x =8 and we got:

`y(8) = 3.529*8 + 37.91= 66.142`

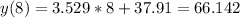
And we can predict the sales representative travelled 11 miles replacing x =11 and we got:

`y(11) = 3.529*11 + 37.91= 76.729`

Explanation:

For this case we have the following data:

Miles Traveled x: 2,3,10,7,8,15,3,1,11

Sales y :31,33,78,62,65,61,48,55,120

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

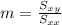
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

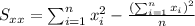
So we can find the sums like this:

`\sum_(i=1)^n x_i =60`

`\sum_(i=1)^n y_i =553`

`\sum_(i=1)^n x^2_i =582`

`\sum_(i=1)^n y^2_i =39653`

`\sum_(i=1)^n x_i y_i =4329`

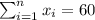
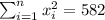
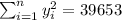
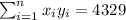
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=582-(60^2)/(9)=182`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=4329-(60*553)/(9)=642.33`

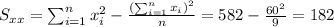
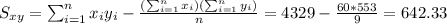
And the slope would be:

`m=(642.33)/(182)=3.529`

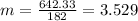
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(60)/(9)=6.67`

`\bar y= (\sum y_i)/(n)=(553)/(9)=61.44`

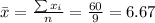
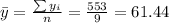
And we can find the intercept using this:

`b=\bar y -m \bar x=61.44-(3.529*6.67)=37.91`

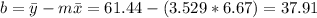
So the line would be given by:

`y=3.529 x +37.91`

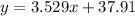
We can predict the sales representative travelled 8 miles replacing x =8 and we got:

`y(8) = 3.529*8 + 37.91= 66.142`

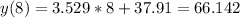
And we can predict the sales representative travelled 11 miles replacing x =11 and we got:

`y(11) = 3.529*11 + 37.91= 76.729`