Answer:
a. D'(p) = -10p - 6
b. There is a decrease of 96 units of demand for each dollar increase
Explanation:
The demand function is:
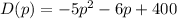
(a) The derivate of the demand function with respect to price gives us the rate of change of demand:
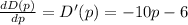
(b) When p = $9, the rate of change of demand is:
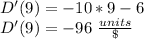
This means that, when p = $9, there is a decrease of 96 units of demand for each dollar increase.