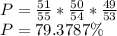Answer:
(a) 0.0152%
(b) 1.1663%
(c) 19.4297%
(d) 79.3787%
Explanation:
Tickets bought by organizers = 4
Number of tickets = 55
Prizes = 3
(a) The probability that the four organizers win all of the prizes is:
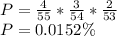
(b) The probability that the four organizers win exactly two of the prizes is:
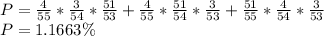
(c) The probability that the four organizers win exactly one of the prizes is:
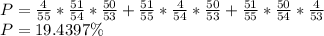
(d) The probability that the four organizers win none of the prizes is: