Question

A history class is comprised of 7 female and 10 male students. If the instructor of the class randomly chooses 7 students from the class for an oral exam, what is the probability that 5 female students and 2 male students will be selected? Round your answer to 3 decimal places.

Answer 1

The probability of selecting 5 female and 2 male students is 0.052.

Explanation:

The class comprises of 7 female students and 10 male students.

Total number of students: 17.

Number of female students, 7.

Number of male students, 10.

The probability of an event E is:

`P(E)=(Favorable\ outcomes)/(Total\ number\ of] outcomes)`

The number of ways to select 7 students from 17 is:

`N ={17\choose 7}=(17!)/(7!(17-7)!)= 19448`

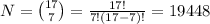
The number of ways to select 5 female students of 7 females is:

`n(F) ={7\choose 5}=(7!)/(5!(7-5)!)= 21`

The number of ways to select 2 male students of 10 males is:

`n(M) ={10\choose 2}=(10!)/(2!(10-2)!)= 45`

Compute the probability of selecting 5 female and 2 male students as follows:

P (5 F and 2 M) = [n (F) × n (M)] ÷ N

`=(21*45)/(19448) \\=0.05183\\\approx0.052`

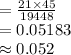
Thus, the probability of selecting 5 female and 2 male students is 0.052.