Question

A one-parameter family of solutions of the DE P' = P( 1 - P) is given below. P = c1et/1 + c1et Does any solution curve pass through the point (0, 6)? Through the point (0, 1)? (If yes, give the corresponding value of C1. If not, enter DNE.) (0, 6) (0, 1)

Answer 1

a. The curve
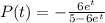`P(t) = -(6e^t)/(5-6e^t)` passes through the point (0, 6)

b. No solution of the curve
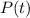`P(t)` passes through the point (0, 1)

Explanation:

Consider the family of the solution of DE
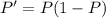`P' = P(1 - P)` is
`P = (c_1e^t)/(1 + c_1e^t)`

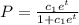
a. If any solution passes through the point (0, 6), then there is
`c_1` such that the point (0, 6) satisfies the solution
`P = (c_1e^t)/(1 + c_1e^t)`

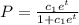
Substitute
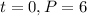`t = 0, P = 6` in
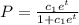`P = (c_1e^t)/(1 + c_1e^t)` and then solve the equation to obtain
`c_1`

`P(t) = (c_1e^t)/(1 + c_1e^t)\\P(0) = (c_1e^0)/(1+c_1e^0)\\ 6 = (c_1)/(1 + c_1)\\ c_1 = -(6)/(5)`

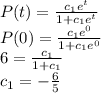
Therefore, the curve
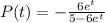`P(t) = -(6e^t)/(5 - 6e^t)` passes through the point (0, 6)

b. If any solution passes through the point(0, 1), then there is
`c_1` such that the point (0, 1) satisfies the solution
`P = (c_1e^t)/(1+c_1e^t)`

`P(t) = (c_1e^t)/(1 + c_1e^t)\\ P(0) = (c_1e^0)/(1 + c_1e^0)\\ 1 = (c_1)/(1+c_1) \\1 + c_1 = c_1`

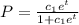
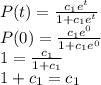
this is not possible

Hence, there is no curve
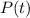`P(t)` that exists which passes through the point (0, 1)