Question

Which of the following equations defines a line that is parallel to the line begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . minus 4 . . . end equation and passes through the point begin ordered pair . . . 3 . . . comma . . . negative 1 . . . end ordered pair?

A
begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . minus 1 . . . end equation

B
begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . minus 3 . . . end equation

C
begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . plus 1 . . . end equation

D
begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . plus 3 . . . end equation

Answer 1

Option D

`y=-(4)/(3)x+3`

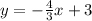
Explanation:

step 1

we have

`y=-(4)/(3)x-4` ----> given line

we know that

If two lines are parallel, then their slopes are equal

so

The slope of the given line is

`m=-(4)/(3)`

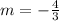
That means

The slope of the line parallel to the given line is also

`m=-(4)/(3)`

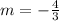
step 2

Find the equation of the line in slope intercept form

`y=mx+b`

where

m is the slope

b is the y-intercept

we have

`m=-(4)/(3)`

`point\ (3,-1)`

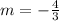
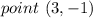
substitute in the linear equation and solve for b

`-1=-(4)/(3)(3)+b`

`-1=-4+b\\b=3`

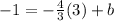
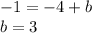
The linear equation is

`y=-(4)/(3)x+3`

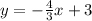
therefore

begin equation . . . y equals . . . begin fraction . . . negative 4 over 3 . . . end fraction, times x . . . plus 3 . . . end equation