Answer:
Step-by-step explanation:
velocity of projection, u = 19 m/s
angle of projection, θ = 34.5°
The horizontal component of velocity remains same as there is no acceleration in the horizontal direction.
So, horizontal component of velocity is given by
ux = u Cos θ
ux = 19 Cos 34.5
ux = 15.66 m/s
Let the ball remains in air for time T.
Use the formula for time of flight.
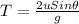
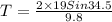
t = 2.2 seconds