Question

A swimming pool has the shape of a box with a base that measures 30 m by 12 m and a uniform depth of 2.2 m. How much work is required to pump the water out of the pool when it is​ full? Use 1000 kg divided by m cubed for the density of water and 9.8 m divided by s squared for the acceleration due to gravity.

Answer 1

853776 J

Step-by-step explanation:

The work-energy needs to pump water out of the pool is the product of the weight of water and distance h

E = Wh = mgh

Since water mass is a body of water we can treat it as the product of density 1000kg/m3 and volume, which is the product of base area and uniform height h

`m = \rho V = \rho \int\limits^(2.2)_0 {A} \, dh`

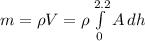
Therefore:

`E = mgh = g\rho A\int\limits^(2.2)_0 {h} \, dh\\E = 9.8*1000*30*12[h^2/2]^(2.2)_0 = 1764000(2.2^2 - 0^2) = 853776 J`