Step-by-step explanation:
(a) As the given chemical reaction equation is as follows.
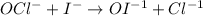
So, when we double the amount of hypochlorite or iodine then the rate of the reaction will also get double. And, this reaction is "first order" with respect to hypochlorite and iodine.
Hence, equation for rate law of reaction will be as follows.
Rate =
![K * [OCl^(-)] * [l^(-)]](https://img.qammunity.org/2021/formulas/chemistry/college/atp8qng8x403li974b6eyrpj2hezt8nldv.png)
(b) Since, the rate equation is as follows.
Rate =
![K [OCl^(-)][l^(-)]](https://img.qammunity.org/2021/formulas/chemistry/college/c7dug09opf1yltr0znmt1ppo8rbx9bl47c.png)
Let us assume that (
![[OCl^(-)] = [l^(-)]](https://img.qammunity.org/2021/formulas/chemistry/college/bsht6gi800a6q2q6th8ym0xshe6q3cc9xq.png) )
)
Putting the given values into the above equation as follows.
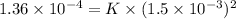
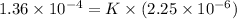
K =

=
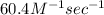
Hence, the value of rate constant for the given reaction is
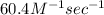 .
.
(c) Now, we will calculate the rate as follows.
Rate =
![K [OCl^(-)][l^(-)]](https://img.qammunity.org/2021/formulas/chemistry/college/c7dug09opf1yltr0znmt1ppo8rbx9bl47c.png)
=
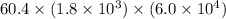
=
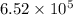
Therefore, rate when
![[OCl^(-)] = 1.8 * 10^(3)](https://img.qammunity.org/2021/formulas/chemistry/college/5t5mtkvzz4ht6unr65q70uz8l84d54nnfp.png) M and
M and
![[I^(-)]= 6.0 * 10^(4)](https://img.qammunity.org/2021/formulas/chemistry/college/eiobfs2dza7rs8h3peqmyeefcvai0h1oil.png) M is
M is
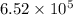 .
.