Question

Consider two bonds, a 3-year bond paying an annual coupon of 12%, and a 20-year bond, also with an annual coupon of 12%. Both bonds currently sell at par value. Now suppose that interest rates rise and the yield to maturity of the two bonds increases to 16%. a. What is the new price of the 3-year bond? (Round your answer to 2 decimal places.) b. What is the new price of the 20-year bond? (Round your answer to 2 decimal places.) c. Do longer or shorter maturity bonds appear to be more sensitive to changes in interest rates? Longer Shorter

Answer 1

longer bonds will be more sensitive to change in interest rate as their cash flow are mor exposed to interest related to short.term bonds. Notice the PV of the maturiry values for each one to notice the greater difference.

3-year bonds $ 910.16

20-year bonds: $ 762.85

Step-by-step explanation:

3-years bonds if rate increase to 16% then:

PV of the coupon payment

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 120.00

time 3

rate 0.16

`120 * (1-(1+0.16)^(-3) )/(0.16) = PV\\`

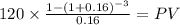
PV $269.5067

PV of maturity

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $1,000.0000

time 3

rate 0.16000

`(1000)/((1 + 0.16)^(3) ) = PV`

PV 640.6577

PV c $269.5067

PV m $640.6577

Total $910.1644

20-years bonds:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 120.00

time 20

rate 0.16

`120 * (1-(1+0.16)^(-20) )/(0.16) = PV\\`

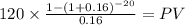
PV $711.4609

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity $1,000.0000

time 20.00

rate 0.16000

`(1000)/((1 + 0.16)^(20) ) = PV`

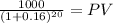
PV 51.3855

PV c $711.4609

PV m $51.3855

Total $762.8464