Answer:

If we use the probability mass function we got:

Explanation:
Previous concepts
The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:
Solution to the problem
Let X the random variable that represent the number of students arrive at the office hour. We know that
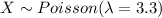
The probability mass function for the random variable is given by:
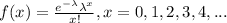
And f(x)=0 for other case.
For this distribution the expected value is the same parameter


And we want this probability:

If we use the probability mass function we got:
