Question

Suppose it takes 4 erg of work to stretch a spring 10 cm beyond its natural length. How much more work is needed to stretch it 4 cm further?

Answer 1

3.84 erg

Step-by-step explanation:

According to Hooke's law, the energy required to stretch a spring by x length is

`E = kx^2/2`

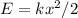
where k is the spring constant. We can plug in E = 4 and x = 10 to estimate k

`4 = k10^2/2`

`4 = 50k`

`k = 4 / 50 = 0.08`

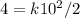
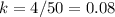
To stretch 4cm further (at 14cm), the total work required is

`E_2 = kx_2^2 = 0.08*14^2/2 = 7.84`

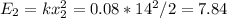
The additional work needed is 7.84 - 4 = 3.84 erg