Question

Use the null hypothesis H0 : μ = 98.6, alternative hypothesis Ha: μ < 98.6, and level of significance α = 0.05. 98 99.6 97.8 97.6 98.7 98.4 98.9 97.1 99.2 97.4 99.1 96.9 98.8 99.9 96.8 97 98.7 97.6 98.7 98.2 whats the t-score?

Answer 1

The t-score is -1.8432

Explanation:

We are given the following in the question:

98, 99.6, 97.8, 97.6, 98.7, 98.4, 98.9, 97.1, 99.2, 97.4, 99.1, 96.9, 98.8, 99.9, 96.8, 97, 98.7, 97.6, 98.7, 98.2

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

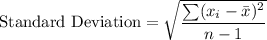
where
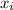`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(1964.4)/(20) = 98.22`

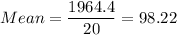
Sum of squares of differences = 16.152

`s = \sqrt{(16.152)/(49)} = 0.922`

Population mean, μ = 98.6

Sample mean,
`\bar{x}` = 98.22

Sample size, n = 20

Sample standard deviation, s = 0.922

First, we design the null and the alternate hypothesis

`H_(0): \mu = 98.6\\H_A: \mu < 98.6`

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

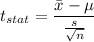
Putting all the values, we have

`t_(stat) = \displaystyle(98.22 - 98.6)/((0.922)/(√(20)) ) = -1.8432`

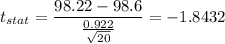
The t-score is -1.8432