Question

At 373.15K and 1 atm, the molar volume of liquid water and steamare 1.88 X 10-5 m3 and 3.06 X 10-2m3, respectively. Given that the heat of vaporization ofwater is 40.79 kJ/mol, calculate the values of ?H and ?Ufor 1 mole in the following process:

H2O (l, 373.15 K, 1 atm) ---> H2O(g, 373.15 K, 1 atm)

Answer 1

Answer The value of
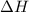`\Delta H` and
`\Delta U` is, 40.79 kJ and 37.7 kJ respectively.

Explanation :

Heat released at constant pressure is known as enthalpy.

The formula used for change in enthalpy of the gas is:

`\Delta Q_p=\Delta H=40.79kJ/mol`

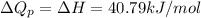
Now we have to calculate the work done.

Formula used :

`w=-P\Delta V\\\\w=-P* (V_2-V_1)`

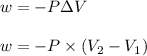
where,

w = work done = ?

P = external pressure of the gas = 1 atm

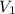`V_1` = initial volume =
`1.88* 10^(-5)m^3=1.88* 10^(-5)* 10^3L=1.88* 10^(-2)L`

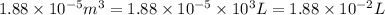
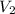`V_2` = final volume =
`3.06* 10^(-2)m^3=3.06* 10^(-2)* 10^3L=3.06* 10^(1)L`

Now put all the given values in the above formula, we get:

`w=-(1atm)* (3.06* 10^(1)-1.88* 10^(-2))L`

`w=-30.5812L.atm=-30.5812* 101.3J=-3097.87556J=-3.09* 10^3J=-3.09kJ`

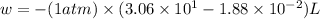
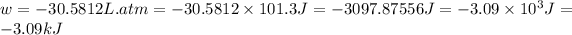
Now we have to calculate the change in internal energy.

`\Delta U=q+w`

`\Delta U=40.79kJ+(3.09kJ)`

`\Delta U=37.7kJ`

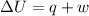
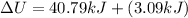
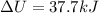
Thus, the value of
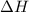`\Delta H` and
`\Delta U` is, 40.79 kJ and 37.7 kJ respectively.