Option A:
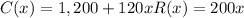 is the equation.
is the equation.
Step-by-step explanation:
Let x represents the number of hours per month the store is open.
It is given that the the monthly rent(expense) = $1200
Also, the employee salary for each hour(expense) = $120x
Thus, the total expense C(x) is
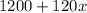
It is also given that the income per hour(revenue) is $200x
Thus, the revenue function R(x) is

The break - even point is given by
Total expense = Revenue
Thus,
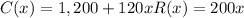 is the equation.
is the equation.
Hence, Option A is the correct answer.