Question

A water tank filled with water to a depth of 16 ft has in inspection cover (1 in. 3 1 in.) at its base, held in place by a plastic bracket. The bracket can hold a load of 9 lbf. Is the bracket strong enough? If it is, what would the water depth have to be to cause the bracket to break?

Answer 1

`F=6.88 [lbf]`

The bracket is strong enough.

`h=20.91 [ft]`

Step-by-step explanation:

Let's recall that the variation of the pressure respect to displacement in a liquid incomprehensible and static will be:

`(dP)/(dy)=-\rho g`

If we take ρ (density) as a constant and solving this differential equation, we will have:

`\Delta P=\rho gh`

• P is the total pressure
• h is the height

Now, the pressure at the base will be:

`P_(base)=\rho gh`

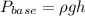
We use this equation knowing that we have atmospheric pressure on the outside of the tank.

The force on the inspection cover will be (A=1 in²):

`F=P_(base)A=\rho ghA= 62.4 [lb/ft^(3)]*32.2 [ft/s^(2)]*16 [ft]*0.00689 [ft^(2)]=221.47 [(lb*ft)/(s^(2))]`

We know that 1 lbf = 32.17 (lb*ft)/s², so:

`F=6.88 [lbf]`

The statement says that the bracket can hold a load of 9 lbf, therefore the bracket is strong enough.

We can use the equation of the force to find the depth.

`F=\rho ghA`

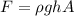
If we solve it for h we will have:

`h=(F)/(\rho gA)`

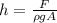
• F is the force that bracket can hold (9 lbf or 289.53 (lb*ft)/s²)
• A is the area (A=0.00689 ft²)

`h=(289.53)/(62.4*32.2*0.00689)=20.91 [ft]`

I hope it helps you!