Question

A conducting sphere with a radius of 0.25 m has a total charge of 5.90 mC. A particle with a charge of −1.70 mC is initially 0.35 m from the sphere's center and is moved to a final position 0.48 m from the sphere's center.

a. What is the difference in electric potential between the particle's final and initial positions, ΔV = Vf − Vi?
b. What is the change in the system's electric potential energy?

Answer 1

Step-by-step explanation:

The given data is as follows.

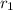`r_(1)` = 0.25 m, q = 5.90 mC =
`5.90 * 10^(-3) C`

`r_(2)` = 0.35 m, q = 1.70 mC =
`1.70 * 10^(-3) C`

(a) Now, we will calculate the electric potential as follows.

V =
`k (q)/(r)`

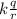
First, we will calculate the initial and final electric potential as follows.

`V_(i) = 9 * 10^(9) * (5.90 * 10^(-3))/(0.25 m)`

=
`212.4 * 10^(6)`

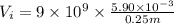
or, =
`2.124 * 10^(8)`

`V_(f) = 9 * 10^(9) * (1.70 * 10^(-3))/(0.35 m)`

=
`43.71 * 10^(6)`

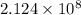
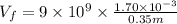
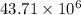
or, =
`4.371 * 10^(8)`

Hence, the value of change in electric potential is as follows.

`\Delta V = V_(f) - V_(i)`

=
`4.371 * 10^(8) - 2.124 * 10^(8)`

=
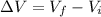
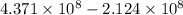
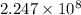`2.247 * 10^(8)` V

Therefore, the difference in electric potential energy is
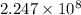`2.247 * 10^(8)` V.

(b) Now, we will calculate the potential energy as follows.

P.E = qV

=
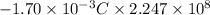`-1.70 * 10^(-3)C * 2.247 * 10^(8)` V

=
`-3.8199 * 10^(5)`

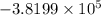
Therefore, the change in the system's electric potential energy is
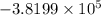`-3.8199 * 10^(5)`.