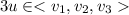Question

Let {v1,v2,v3} be a set of vectors in Rn . If u is Span {v1,v2,v3}, show that 3u is in Span {v1,v2,v3}.(Hint: since you are told that u is in the span {v1,v2,v3}, you can automatically say that there are scalars c1,c2 and c3 so that u = c1v1+c2v2+c3v3. Your goal now is to find a way to write 3u as a linear combination of {v1,v2,v3}

Answer 1

See proof below

Explanation:

We will use the hint. The statement of the hint holds true, as the linear span of a set of vectors T is equal to the set of linear combinations of vectors in T.

Denote the linear span of vectors with the curly brackets < >, that is,
`span\{v_1,v_2,v_3\}:=<v_1,v_2,v_3>`

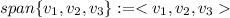
Let
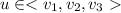`u\in <v_1,v_2,v_3>`, then u is a linear combination of v1,v2,v3, that is, there exist scalars
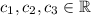`c_1,c_2,c_3\in \mathbb{R}` such that
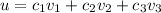`u=c_1v_1+c_2v_2+c_3v_3`. Multiply by 3 in both sides to get
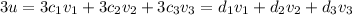`3u=3c_1v_1+3c_2v_2+3c_3v_3=d_1v_1+d_2v_2+d_3v_3`, with
`d_i=3c_i,i=1,2,3`

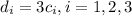
Since
`c_1,c_2,c_3\in \mathbb{R}`,
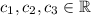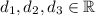`d_1,d_2,d_3\in \mathbb{R}` as real numbers are closed under multiplication. Therefore 3u is a linear combination of the vectors
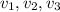`v_1,v_2,v_3`, that is,
`3u\in <v_1,v_2,v_3>`