Question

Write the equation of the perpendicular bisector of PQ. A) y = 1 B) x = 1 C) y = x D) y = x + 1

Answer 1

Answer: y=1

Explanation:

Answer 2

Answer: Since the exercise is incomplete, I'll give you the general steps to find the equation of the perpendicular bisector of PQ (See explanation).

Explanation:

1. You need to find the midpoint of PQ with the following formula:

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

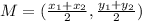
2. Then, you must find the slope of PQ with this formula:

`m=(y_2-y_1)/(x_2-x_1)`

3. By definition, the slopes of perpendicular lines are negative reciprocals. Knowing that, determine the slope of of the perpendicular bisector.

4. Remember that the Slope-Intercept form of a line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Substitute the slope of the perpendicular bisector and the coordinates of the midpoint of PQ into the equation
`y=mx+b`.

5. Solve for "b".

6. Finally, substitute the values of "m" and "b" into
`y=mx+b`, in order to get the equation of the perpendicular bisector of PQ.