Question

In a room full of air, the air is mainly composed of Nitrogen and Oxygen molecules (both at room temperature). Find (to two significant figures) the values of vrms for both molecules. (Eq. (20.26) relates vrms to absolute temperature.

Answer 1

Step-by-step explanation:

Expression for the
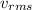`v_(rms)` speed is as follows.

`v_(rms) = \sqrt{(3kT)/(M)}`

where,
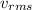`v_(rms)` = root mean square speed

k = Boltzmann constant

T = temperature

M = molecular mass

As the molecular weight of oxygen is 0.031 kg/mol and R = 8.314 J/mol K. Hence, we will calculate the value of
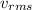`v_(rms)` as follows.

`v_(rms) = \sqrt{(3kT)/(M)}`

=
`\sqrt{(3 * 8.314 J/mol K * 309.02 K)/(0.031 kg/mol)}`

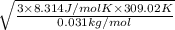
= 498.5 m/s

Hence,
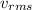`v_(rms)` for oxygen atom is 498.5 m/s.

For nitrogen atom, the molecular weight is 0.028 kg/mol. Hence, we will calculate its
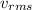`v_(rms)` speed as follows.

`v_(rms) = \sqrt{(3kT)/(M)}`

=
`\sqrt{(3 * 8.314 J/mol K * 309.92 K)/(0.028 kg/mol)}`

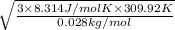
= 524.5 m/s

Therefore,
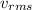`v_(rms)` speed for nitrogen is 524.5 m/s.