Question

Given the sequence 2, 4, 8, , 16,........, where x = 0, 1, 2, 3, .......what is the function rule? f(x) = 2x + 2 f(x) = 2(2)x f(x) = (2x) f(x) = 2

Answer 1

Option C:
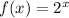`f(x)=2^x` is the function rule.

Step-by-step explanation:

The sequence is
`2,4,8,16, \dots \dots`

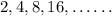
Let us find the common difference of this sequence.

Common ratio =
`(4)/(2) =2`

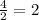
Hence,
`r=2`

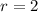
Thus, the given sequence is a geometric progression.

To determine the function rule, let us substitute the values in the general formula of GP which is given by

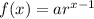`f(x)=ar^(x-1)` where
`a=2, r=2`

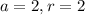
Substituting we get,

`f(x)=2(2)^(x-1)`

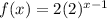
Simplifying, we get,

`f(x)=2*2^x*2^{-1`

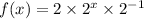
Adding the powers, we get,

`f(x)=2^(1+x-1)`

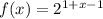
Simplifying, we get,

`f(x)=2^x`

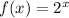
Hence, the function rule is
`f(x)=2^x`

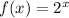
Thus, Option C is the correct answer.