Answer:
- No, I do not agree because the monthly payments are calculated using 9% interest compounded montly, and the student is calculating using simple interest.
Step-by-step explanation:
The question is missing the last part. Thus, I copy the complete question for fully understanding:
- A student looking at the timeline for a student loan on page 60 of the text makes the following observation: The text states that the interest rate on the loan is 9%, but this calculation is obviously wrong. Each monthly payment is $127×12 = $1,524 per year. Therefore, because the principal of the loan is $10,000, the interest rate must be $1,524/ $10,000 = 0.1524 or 15.24%.
Briefly explain whether you agree with the student's reasoning.
Answer
The payments of a loan are calculated using compound interest. The formula to calculate the monthly payments is:
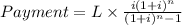
Where:
- Payment is the monthly payment
- L is the amount of the loan (principal)
- i is the monthly interest rate (the annual interest rate divided by 12)
- n is the number of months
You can obtain the monthly payment of $127 with a an interest rate of 9%, for a $10,000 loan over 10 years, using previous formula:
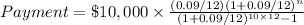
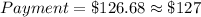
The student then will pay $127 × 12 = $1524 per year, but that cannot be used to calculate the annual interest using a simple ratio, which would be valid only for simple interest.