Question

If I measure a set of times with a mean of 1.4 s, a standard deviation of 0.6 s, and an SDOM of 0.2 s, how should I report my measurement?

Answer 1

The measurements should be reported as 1.4s ± 0.2s.

Explanation:

The mean of a data set consisting of n independent values is:

`\bar X=(1)/(n)\sum (x_(1)+x_(2)+x_(3)...+x_(n))`

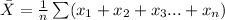
The standard deviation of a data set consisting of n independent values is the measure of the spread of the data. It is computed as follows:

`\sigma=\sqrt{(1)/(n)\sum(X_(i)-\bar X)^(2)}`

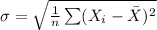
The standard deviation of mean (SDOM) is also known as the standard error.

The standard error is:

`\delta X=\frac{\sigma}{\sqrt {n}}`

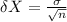
If we want to report these measurements the format is:
`\bar X\pm \delta X`

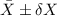
Given:

`\bar X=1.4s\\\delta =0.2s`

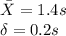
These measurements can be reported as:

`\bar X\pm \delta X=1.4s\pm 0.2s`

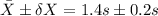
Thus, the measurements should be reported as 1.4s ± 0.2s.