Question

If we draw some dots on a paper, and connect each one of them to every other one with a single line, how many lines will we draw? Using mathematical induction, prove that the number of lines for n dots is 1, 2, ........., n(n − 1).

Answer 1

Explanation:

Let us assume that we have n different dots on a paper. We are to connect pairwise by a line. We have to find out how many lines can be formed.

Let us prove by induction.

If there is one dot then we have no line = 1(1-1) =0

Thus n(n-1) is true for 1 dot

Let us assume that for n dots we have n(n-1) lines

Add one more point now total points are n+1.

Already the existing n points are connected by a line.

So the extra point has to be connected to each of n point

i.e. n lines should be added from the new point to the n points and again n lines from the points to the new point(Assuming lines are different if initial and final point are different)

So 2n lines would be added

So total number of lines for n+1 points

`= n(n-1) +n+n= n^2-n+2n \\= n^2+n\\=n(n+1)`

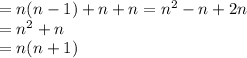
Thus true for n+1 if true for n. Already true for n =1

So proved by induction for all natural numbers n.