Question

In an experiment, a certain colony of bacteria initially has a population of 50,000. A reading is taken every 2 hours, and at the end of every 2-hour interval, there are 3 times as many bacteria as before. a. Write a recursive definition for A(n), the number of bacteria present at the beginning of the nth time period. b. At the beginning of which interval are there 1,350,000 bacteria present?

Answer 1

1) Recursive definition:
`p_n = (50,000)3^n`

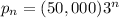
2) At the beginning of the 4th interval

Step-by-step explanation:

1)

The initial population of the bacteria at time zero is

`p_0 = 50,000`

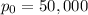
Here we are told that the reading is taken every two hours; we call this time interval "n", so

`n=2 h`

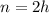
And also, after every time interval n, the number of bacteria has tripled.

This means that when n = 1,

`p_1 = 3 p_0`

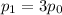
And when n=2,

`p_2 = 3 p_1 = 3(3p_0)=9 p_0`

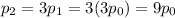
Applied recursively, we get

`p_n = 3^n p_0`

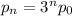
And substituting p0,

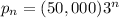`p_n = (50,000)3^n` (1)

2)

Here we want to find at the beginning of which interval there are

`p=1,350,000`

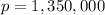
bacteria.

This means that we can rewrite eq.(1) as

`1,350,000=(50,000)3^n`

By simplifying,

`27=3^n`

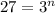
Which means that

`n=3`

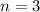
However, this means that the number of bacteria is 1,350,000 after 3 time intervals; therefore, at the beginning of the 4th interval.