Question

Your local grocery store sells 5 lb bags of potatoes. However, the 5 lb bags do not weight exactly 5 lbs. If we let Xi be the weight of a randomly selected 5 lb bag of potatoes, historical data indicates that Xi ~ N(5.36, 0.14). The local warehouse store sells 10 lb bags of potatoes, which also do not weight exactly 10 lbs. If Y is the weight of a randomly selected 10 lb bag, historical data indicates that Y ~ N(10.22, 0.18). We randomly select two 5 lb bags of potatoes and one 10 lb bag of potatoes. What is the probability that the sum of the weights of the two 5 lb bags exceeds the weight of one 10 lb bag?

Answer 1

The probability that the sum of the weights of the two 5 lb bags exceeds the weight of one 10 lb bag is 0.719.

Explanation:

The random variable
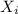`X_(i)` denote the weight of a 5 lb bag.

The random variable
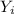`Y_(i)` denote the weight of a 10 lb bag.

It is provided that:

`X_(i)\sim N(5.36, 0.14)\\Y_(i)\sim N(10.22, 0.18)`

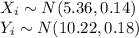
Let A = X + X and B = A - Y

The random variable A also follows a Normal distribution because the sum of two normal random variables is normal.

Similarly B also follows a normal distribution because the difference of two normal random variables is normal.

Compute the mean and variance of A as follows:

`E(A)=E(X+X)=E(2X)=2E(X)=2*5.36=10.72\\V(A)=V(X+X)=V(2X)=2^(2)V(X)=4*0.14=0.56`

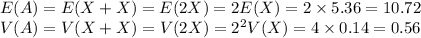
Compute the mean and variance of B as follows:

`E(B)=E(A-Y)=E(A)-E(Y)=10.72-10.22=0.50\\V(B)=V(A-Y)=V(A)+V(Y)-2Cov(A,Y)=V(A)+V(Y)=0.56+0.18=0.74`

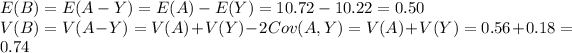
Compute the probability that the sum of the weights of the two 5 lb bags exceeds the weight of one 10 lb bag, i.e. P (A > Y)

`P(A>Y)=P(A-Y>0)\\=P(B>0)\\=P((B-E(B))/(√(V(B)))>(0-0.50)/(√(0.74)) )\\=P(Z>-0.581)\\=P(Z<0.581)\\=0.719`

**Use the standard normal table for the probability value.

Thus, the probability that the sum of the weights of the two 5 lb bags exceeds the weight of one 10 lb bag is 0.719.