Question

A survey of 90 men found that an average amount spent on St. Patrick's day of $55 with a standard deviation of $18. A similar survey of 86 women found they spent an average of $44 with a standard deviation of $16. When testing the hypothesis (at the 5% level of significance) that men spend more than women on St. Patrick's day, what is the test statistic?

Answer 1

The value of the test statistic is 4.70.

Explanation:

The hypothesis for this test can be defined as follows:

H₀: Men do not spend more than women on St. Patrick's day, i.e. μ₁ = μ₂.

Hₐ: Men spend more than women on St. Patrick's day, i.e. μ₁ > μ₂.

The population standard deviations are not known.

So a t-distribution will be used to perform the test.

The test statistic for the test of difference between mean is:

`t=\frac{\bar x_(1)-\bar x_(2)}{\sqrt{(s^(2)_(1))/(n_(1))+(s^(2)_(2))/(n_(2))} }`

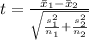
Given:

`\bar x_(1)=55\\s_(1)=18\\n_(1)=90\\\bar x_(1)=44\\s_(1)=16\\n_(1)=86`

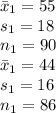
Compute the value of the test statistic as follows:

`t=\frac{\bar x_(1)-\bar x_(2)}{\sqrt{(s^(2)_(1))/(n_(1))+(s^(2)_(2))/(n_(2))} }=\frac{55-44}{\sqrt{(15^(2))/(90)+(16^(2))/(86) }}=4.70`

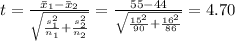
Thus, the value of the test statistic is 4.70.