Answer:
6.56% probability that a real emergency situation exists.
Explanation:
We have these following probabilities:
A 0.4% probability that a real emergency situation exists.
A 99.6% probability that a real emergency situation does not exist.
If an emergency situation exists, a 95% probability that the alarm sounds.
If an emergency situation does not exist, a 2% probability that the alarm sounds.
The problem can be formulated as the following question:
What is the probability of B happening, knowing that A has happened.
It can be calculated by the following formula
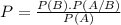
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
In this problem:
What is the probability of a real emergency situation existing, given that the alarm has sounded.
P(B) is the probability of there being a real emergency situation. So
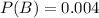 .
.
P(A/B) is the probability of the alarm sounding when there is a real emergency situation. So P(A/B) = 0.95.
P(A) is the probability of the alarm sounding. This is 95% of 0.4%(real emergency situation) and 2% of 99.6%(no real emergency situation). So
P(A) = 0.95*0.04 + 0.02*0.996 = 0.05792
Given that the alarm has just sounded, what is the probability that a real emergency situation exists?
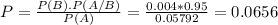
6.56% probability that a real emergency situation exists.