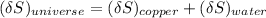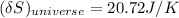Answer:
the entropy change of the copper block = - 117.29 J/K
the entropy change of the water = 138.01 J/K
the entropy change of the universe = 20.72 J/K
Step-by-step explanation:
For Copper block:
the mass of copper block
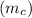 = 1.00 kg
= 1.00 kg
Temperature of block of copper
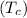 = 100°C
= 100°C
= (100+273)K
= 373K
Standard Heat capacity for copper
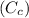 = 386 J/kg.K
= 386 J/kg.K
For water:
We know our volume of liquid water to be = 4.00 L
At 0.0°C Density of liquid water = 999.9 kg/m³
As such; we can determine the mass since :
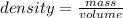
∴ the mass of 4.00 L of liquid water at 0.0°C will be its density × volume.
= 999.9 kg/m³ ×
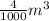
= 3.9996 kg
so, mass of liquid water
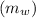 = 3.9996 kg
= 3.9996 kg
Temperature of liquid water
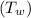 at 0.0°C = 273 K
at 0.0°C = 273 K
Standard Heat Capacity of liquid water
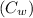 = 4185.5 J/kg.K
= 4185.5 J/kg.K
Let's determine the equilibruium temperature between the copper and the liquid water. In order to do that; we have:
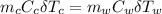

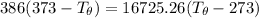
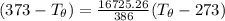
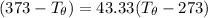
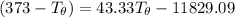
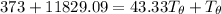
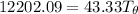

∴ the equilibrium temperature = 275.26 K
NOW, to determine the Entropy change of the copper block; we have:

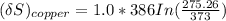
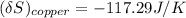
The entropy change of the water can also be calculated as:
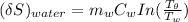
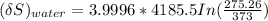
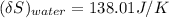
The entropy change of the universe is the combination of both the entropy change of copper and water.