Answer:
49.32% probability that the proportion in our sample of green candies will be more than 25%.
Explanation:
For each candy, there are only two possible outcomes. Either it is green, or it is not. The probabilities of each candy being green are independent from each other. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
In this problem we have that:
According to the manufacturer of the candy Skittles, 25% of the candy produced are green. This means that
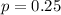
If we take a random sample of 10 bags of Skittles, what is the probability that the proportion in our sample of green candies will be more than 25%?
10 bags, so

This is
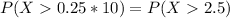
The number of bags is a discrete number, so
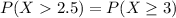 .
.
Either the number of green bags is lower than 3, or it is greater or equal than 3. The sum of these probabilities is decimal 1. Mathematically, this means that:
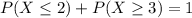
We want
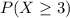 . So
. So
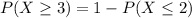
In which

So

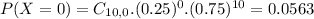
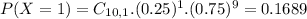
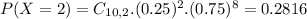
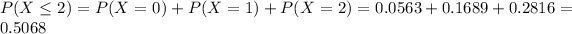
Then
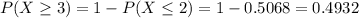
49.32% probability that the proportion in our sample of green candies will be more than 25%.