Question

This week, one of the topics is describing sampling distributions. In project 2 you will be using female heights to answer a variety of questions. As practice for this project, please address the bulleted items below for male heights. It will be necessary to know that the average height for men is assumed to be 70 inches with a standard deviation of 4 inches. To receive full credit, you also need to comment on two other posts from your classmates (you can just state whether or not you agree with their solution and if not, what you did differently).George Washington was 6 feet tall. Find the z-score for George Washington. Find the probability that a randomly selected individual will be as tall or taller than George Washington. Interpret both the z-score and the probability in a sentence.

Answer 1

a) 0.5

b) 0.309

Explanation:

We are given the following information in the question:

Mean, μ = 70 inches

Standard Deviation, σ = 4 inches

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

Height of George Washington = 6 feet =
`6* 12 = 72\text{ inches}`

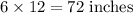
x = 72

a) z-score

`z_(score) = \displaystyle(72-70)/(4) = 0.5`

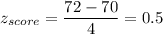
Interpretation:

This, mean that George Washington is 0.5 standard deviation more than the mean height of for men.

b) P(individual will be as tall or taller than George Washington)

`P( x \geq 72) = P( z \geq 0.5)`

`= 1 - P(z < 0.5)`

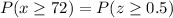
Calculation the value from standard normal z table, we have,

`P(x \geq 72) = 1 - 0.691 = 0.309 = 30.9\%`

Interpretation:

0.309 is the probability that a randomly selected individual will be as tall or taller than George Washington.