Question

Suppose that a basketball player can score on a particular shot with probability .3. Use the central limit theorem to find the approximate distribution of S, the number of successes out of 25 independent shots. Find the approximate probabilities that S is less than or equal to 5, 7, 9, and 11 and compare these to the exact probabilities.

Answer 1

(a) The probability that the number of successes is at most 5 is 0.1379.

(b) The probability that the number of successes is at most 5 is 0.1379.

(c) The probability that the number of successes is at most 5 is 0.1379.

(d) The probability that the number of successes is at most 11 is 0.9357.

→ All the exact probabilities are more than the approximated probability.

Explanation:

Let S = a basketball player scores a shot.

The probability that a basketball player scores a shot is, P (S) = p = 0.30.

The number of sample selected is, n = 25.

The random variable
`S\sim Bin(25,0.30)`

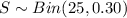
According to the central limit theorem if the sample taken from an unknown population is large then the sampling distribution of the sample proportion (
`\hat p`) follows a normal distribution.

The mean of the the sampling distribution of the sample proportion is:
`E(\hat p)=p=0.30`

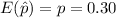
The standard deviation of the the sampling distribution of the sample proportion is:

`SD(\hat p)=\sqrt{( p(1- p))/(n) }=\sqrt{( 0.30(1-0.30))/(25) }=0.092`

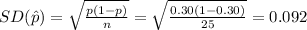
(a)

Compute the probability that the number of successes is at most 5 as follows:

The probability of 5 successes is:
`p=(5)/(25) =0.20`

`P(\hat p\leq 0.20)=P((\hat p-E(\hat p))/(SD(\hat p))\leq (0.20-0.30)/(0.092) )\\=P(Z\leq -1.087)\\=1-P(Z<1.087)\\=1-0.8621\\=0.1379`

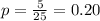
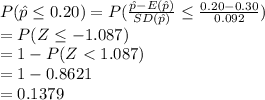
**Use the standard normal table for probability.

Thus, the probability that the number of successes is at most 5 is 0.1379.

The exact probability that the number of successes is at most 5 is:

`P(S\leq 5)={25\choose 5}(0.30)^(5)91-0.30)^(25-5)=0.1935`

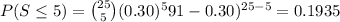
The exact probability is more than the approximated probability.

(b)

Compute the probability that the number of successes is at most 7 as follows:

The probability of 5 successes is:
`p=(7)/(25) =0.28`

`P(\hat p\leq 0.28)=P((\hat p-E(\hat p))/(SD(\hat p))\leq (0.28-0.30)/(0.092) )\\=P(Z\leq -0.2174)\\=1-P(Z<0.2174)\\=1-0.5871\\=0.4129`

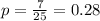
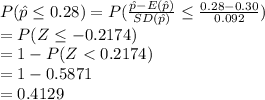
**Use the standard normal table for probability.

Thus, the probability that the number of successes is at most 7 is 0.4129.

The exact probability that the number of successes is at most 7 is:

`P(S\leq 57)={25\choose 7}(0.30)^(7)91-0.30)^(25-7)=0.5118`

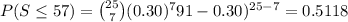
The exact probability is more than the approximated probability.

(c)

Compute the probability that the number of successes is at most 9 as follows:

The probability of 5 successes is:
`p=(9)/(25) =0.36`

`P(\hat p\leq 0.36)=P((\hat p-E(\hat p))/(SD(\hat p))\leq (0.36-0.30)/(0.092) )\\=P(Z\leq 0.6522)\\=0.7422`

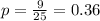
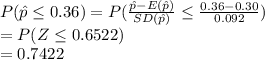
**Use the standard normal table for probability.

Thus, the probability that the number of successes is at most 9 is 0.7422.

The exact probability that the number of successes is at most 9 is:

`P(S\leq 9)={25\choose 9}(0.30)^(9)91-0.30)^(25-9)=0.8106`

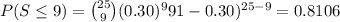
The exact probability is more than the approximated probability.

(d)

Compute the probability that the number of successes is at most 11 as follows:

The probability of 5 successes is:
`p=(11)/(25) =0.44`

`P(\hat p\leq 0.44)=P((\hat p-E(\hat p))/(SD(\hat p))\leq (0.44-0.30)/(0.092) )\\=P(Z\leq 1.522)\\=0.9357`

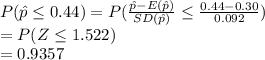
**Use the standard normal table for probability.

Thus, the probability that the number of successes is at most 11 is 0.9357.

The exact probability that the number of successes is at most 11 is:

`P(S\leq 11)={25\choose 11}(0.30)^(11)91-0.30)^(25-11)=0.9558`

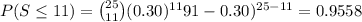
The exact probability is more than the approximated probability.