Question

Se lanza un objeto desde una plataforma.

Su altura (en metros), x segundos después del lanzamiento, está modelada por:
h(x)=-5x^2+20x+60h(x)

¿Cuántos segundos después del lanzamiento el objeto llega al suelo?

Answer 1

6 seconds

Explanation:

The question in English is

An object is thrown from a platform.

Its height (in meters), x seconds after launch, is modeled by:

h(x)=-5x^2+20x+60

How many seconds after the launch does the object reach the ground?

Let

x ----> the time in seconds

h(x) ---> the height of the object

we have

`h(x)=-5x^2+20x+60`

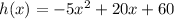
we know that

When the object hit the ground the height is equal to zero

so

For h(x)=0

we have

`-5x^2+20x+60=60`

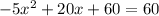
The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

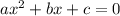
is equal to

`x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}`

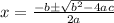
in this problem we have

`-5x^2+20x+60=60`

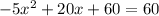
so

`a=-5\\b=20\\c=60`

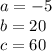
substitute in the formula

`x=\frac{-20\pm\sqrt{20^(2)-4(-5)(60)}} {2(-5)}`

`x=\frac{-20\pm√(1,600)} {-10}`

`x=\frac{-20\pm40} {-10}`

`x=\frac{-20+40} {-10}=-2`

`x=\frac{-20-40} {-10}=6`

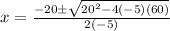
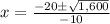
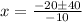
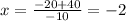
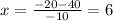
The solution is x=6 sec

The he object reach the ground at x=6 seconds