Question

Find an equation of the set of all points equidistant from the points A(−3, 6, 3) and B(4, 1, −1). Describe the set.

Answer 1

See below

Explanation:

I will describe this set in R³. Let P=(x,y,z) be a point equidistant to A and B, that is, the distance from P to A is equal to the distance from P to B.

First, using the usual distance formula, the distance from P to A is equal to
`d(P,A)=√((x-(-3))^2+(y-6)^2+(z-3)^2)=√((x+3)^2+(y-6)^2+(z-3)^2)`

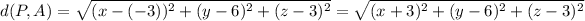
On the other hand, the distance form P to B is equal to
`d(P,B)=√((x-4)^2+(y-1)^2+(z-(-1))^2)=√((x-4)^2+(y-1)^2+(z+1)^2)`

P is equidistant from A and B if and only if P satisfies the equation d(P,A)=d(P,B), that is,

`√((x+3)^2+(y-6)^2+(z-3)^2)=√((x-4)^2+(y-1)^2+(z+-1)^2)`

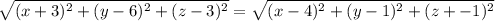
Take the square in both sides of this equation to get

`(x+3)^2+(y-6)^2+(z-3)^2=(x-4)^2+(y-1)^2+(z+1)^2`

`(x+3)^2-(x-4)^2+(y-6)^2-(y-1)^2+(z-3)^2-(z+1)^2=0`

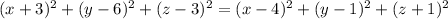
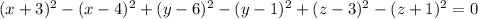
You can simplify using difference of squares and multiplying like this:

`(7)(2x-1)+(-5)(2y-7)+(-4)(2z-2)=0`

`14x-10y-8z+36=0`

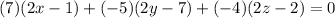
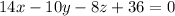
which is the equation of a plane.