Answer:
0.74141
Explanation:
There are 52 cards in total
since each card is different,
the probability = number of favorable cards / total number of outcomes
P(C₁) = number of favorable cards / total number of outcomes
=
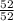
P(C₂, C₁) = number of favorable cards / total number of outcomes
=

P(C₃,C₁ ∩ C₂) =
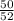
P(C₄,C₁ ∩ C₂ ∩ C₃) =
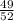
P(C₅,C₁ ∩ C₂ ∩ C₃ ∩ C₄) =
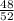
P(C₆,C₁ ∩ C₂ ∩ C₃ ∩ C₄ ∩ C₅) =
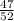
General multiplication rule
P(A) =P(C₁ ∩ C₂ ∩ C₃ ∩ C₄ ∩ C₅ ∩ C₆)
=

= 8,808,975 / 11,881,376
= 0.74141