Answer:
The sample mean is
 .
.
The sample standard deviation is
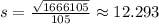 .
.
The lower quartile is 59.
The upper quartile is 75.
The median is
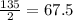 .
.
Explanation:
We have the following data:
83, 45, 61, 40, 83, 67, 45, 66, 70, 69, 80, 58, 68, 60, 67, 72, 73, 70, 57, 63, 70, 78, 52, 67, 53, 67, 75, 61, 70, 81, 76, 79, 75, 76, 58, 31.
(a)
The sample mean of data is given by the formula
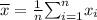 ,
,
where n is the number of values and
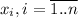 are the values themselves.
are the values themselves.
Since we have 36 points, then n = 36.
The sum of the points is
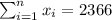 .
.
Therefore, the sample mean is
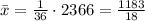 .
.
The sample standard deviation of data is given by the formula
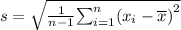 ,
,
where n is the number of values,
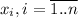 are the values themselves, and
are the values themselves, and
 is the mean of the values.
is the mean of the values.
The mean of the data is
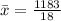 .
.
n = 36.
Sum of
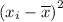 is
is
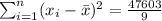 .
.
Now,
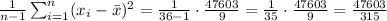
Finally,

(b)
The
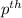 percentile is a value such that at least
percentile is a value such that at least
 percent of the observations is less than or equal to this value and at least (
percent of the observations is less than or equal to this value and at least (
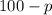 ) percent of the observations is greater than or equal to this value.
) percent of the observations is greater than or equal to this value.
The first step is to sort the values.
The sorted values are 31, 40, 45, 45, 52, 53, 57, 58, 58, 60, 61, 61, 63, 66, 67, 67, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 80, 81, 83, 83.
The lower quartile or 25th percentile is the median of the lower half of the data set.
Now, calculate the index
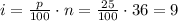
Since the index
 is an integer, the 25th percentile is the average of the values at the positions
is an integer, the 25th percentile is the average of the values at the positions
 and
and
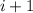 .
.
The value at the position
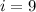 is 58 and at the position
is 58 and at the position
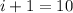 is 60.
is 60.
Their average is:
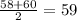 .
.
The lower quartile is 59.
The upper quartile or 75th percentile is the median of the upper half of the data set.
Now, calculate the index
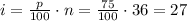
Since the index
 is an integer, the 75th percentile is the average of the values at the positions
is an integer, the 75th percentile is the average of the values at the positions
 and
and
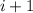 .
.
The value at the position
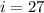 is 75 and at the position
is 75 and at the position
 is 75.
is 75.
Their average is:
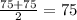 .
.
The upper quartile is 75.
(c) The median is the middle value of the data set. The median value depends on the number of values. If the number of values is odd, then the median is the "central" value among the sorted values. If the number of values is even, then the median is the average of the two "central values".
The first step is to sort the values.
We have 36 values, so their number is even.
Since the number is even, the median is the average of the "central values":
31, 40, 45, 45, 52, 53, 57, 58, 58, 60, 61, 61, 63, 66, 67, 67, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 80, 81, 83, 83.
Calculate the median:
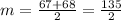 .
.
The median is
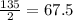 .
.