To solve this problem, we will begin by applying the concept of rotational kinetic energy, defined as the product of half of the Inertia by squared angular velocity. From this relationship we will obtain the value of the angular velocity.
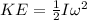
Here,
I = Moment of Inertia
 = Angular velocity
= Angular velocity
Replacing with our values we have that,
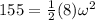
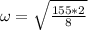
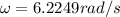
Now through the kinematic equations of angular movement we will find the value of the angular acceleration, since this is equivalent to the change of the angular velocity in a certain time, like this:
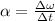
Replacing,
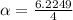
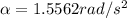
Finally, Torque's definition tells us that this is equivalent to the product between the moment of inertia and angular acceleration, therefore,
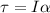
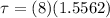
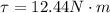
Therefore the torque required is 12.44N-m