Answer:
(1,-8)
Explanation:
We were given three vertices of a parallelogram to be:
(3,-2), (-1,-4), (5,-6).
After plotting the points as shown in the attachment, we realize (3,-2) and (-1,-4) form a diagonal.
The midpoint of this diagonal using the midpoint formula is
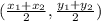
is
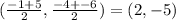
Recall that, the midpoint of both diagonals are the same.
Let the fourth point have coordinates (x,y).
Then using the midpoint formula again with (3,-2), we have:
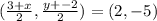
This implies that:
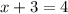 and
and

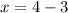 and
and
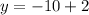
x=1 and y=-8
The coordinates of the fourth point are:
(1,-8)