Question

This problem has been solved!

See the answer
In Problems 1 and 2,y=1/(1+c1e-x) is a one-parameter family ofsolutions of the first-order DE y'=y-y2. Find asolution of the first-order IVP consisting of this differentialequation and the given initial condition.
1. y(0)=-1/3

Answer 1

See below

Explanation:

With the information given, we only need to find the value of the parameter c1 for which the initial condition holds. Assume our solution is of the given form
`y(x)=(1)/(1+c_1e^(-x))`

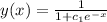
Then
`y(0)=(-1)/(3)=(1)/(1+c_1)`

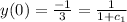
Thus

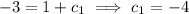`-3=1+c_1\implies c_1=-4`. Therefore, the unique solution to the initial value problem is the function

`y(x)=(1)/(1-4e^(-x))`

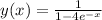
Again, it's important to note that the problem gives us the general solution for granted. If you want to solve another IVP, sometimes you need to find the general solution first, and then find the parameters corresponding to the initial conditions.