Question

A new battery's voltage may be acceptable (A) or unacceptable (U). A certain flashlight requires two batteries, so batteries will be independently selected and tested until two acceptable ones have been found. Suppose that 93% of all batteries have acceptable voltages. Let Y denote the number of batteries that must be tested.

a. What is p(2), that is P(y = 2)?
b. What is p(3)?
c. To have Y = 5, what must be true of the fifth battery selected?

i. The fifth battery must be an A.
ii. The fifth battery must be a U.

Answer 1

a. P(y = 2) = 0.8469

b. p(3) = 0.121

c .To have Y = 5 The fifth battery must be an A.

Explanation:

Given:

93% batteries have acceptable voltages

Let Y denotes the number of batteries that must be tested.

P(acceptable) = P(A)

P(A) = 0.93

P(unacceptable) = P(U)

P(U) = 1- P(A)

P(U) = 1- 0.93

P(U) = 0.07

a. What is p(2), that is P(y = 2)

P(y = 2) = P(AA)

P(AA) = (0.93)(0.093)

P(AA) = 0.8469

b) What is p(3)

The favourable cases to y=3 are AUA, UAA

P(y = 3) = P ( A UA ) + P ( U A A )

P ( A UA ) + P ( U A A ) =
`(0.93* 0.07* 0.93)+(0.07*0.93*0.93)`

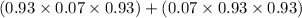
P ( A UA ) + P ( U A A ) =0.0605 + 0.0605

P ( A UA ) + P ( U A A ) = 0.121

(c) To have Y = 5, what must be true of the fifth battery selected?

In order to have y=5 the 5th battery must be second acceptable battery

The favorable outcomes are AUUUA, UUUAA, UAUUA and UUAUA

P(y=5) = P(AUUUA) + P(UUUAA) + P(UAUUA) + P(UUAUA)

`= (0.93 * 0.07 * 0.07 * 0.07 * 0.93)+(0.07 * 0.07* 0.07* 0.93* 0.93) + (0.07 * 0.93* 0.07* 0.07* 0.93)+(0.07* 0.07* 0.93* 0.07* 0.93)`

= 0.008