Question

Rewrite the following differential equation as an equivalent system of first-order differential equations. Use the variables x1=x,x2=x′,x3=x′′,etc. (so that your equations will have the form x′2=x3, etc.: denote subscripts by appending the subscript to the variable name: x1= x1) Equation to rewrite: x(4) + 17x" - 17' + 17x = -9 cos(2t)

Answer 1

See details below

Explanation:

Your equation is
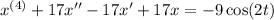`x^((4))+17x''-17x'+17x=-9\cos(2t)`. Solve for the fourth derivative to get
`x^((4))=-17x''+17x'-17x-9\cos(2t)`

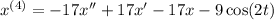
Now apply said change of variables: let
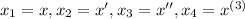`x_1=x,x_2=x',x_3=x'',x_4=x^((3))`. Then, substituting on out first equation, we obtain the system:

`x_4'=-17x_3+17x_2-17x_1-9\cos(2t)`

`x_4=x_3'`

`x_3=x_2'`

`x_2=x_1'`

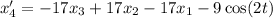
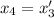
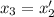
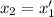
In general, if you have an nth order ordinary differential equation, you can apply the same idea to obtain a system of differential equations with n unknowns. Therefore, solving systems of differential equations is equivalent to solving higher-order differential equations.