Question

Two people are standing on a 2.50-m-long platform, one at each end. The platform floats parallel to the ground on a cushion of air, like a hovercraft. The two people, the platform and a 3.63-kg ball are all initially at rest. One person throws the 3.63-kg ball to the other, who catches it. The ball travels nearly horizontally. Excluding the ball, the total mass of the platform and people is 198 kg. Because of the throw, this 198-kg mass recoils. How far does the platform move before coming to rest again?

Answer 1

The platform move before coming to rest again 0.045 m far

Step-by-step explanation:

Given

Ball is in motion

M (Platform mass + 2 people mass)

V (recoil velocity of the platform)

m (ball mass)

v (velocity ball)

MV + mv = 0

Distance of the platform movement is

t (time that the ball is in the air)

x = Vt

t =
`(L)/(v - V)`

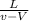
Knowing the platform and the ball are moving while the ball is in the air

x =
`(V)/(v - V) * L`

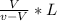
Also knowing that

`(V)/(v) = (-m)/(M)`

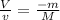
This way,

x =
`(((V)/(v)) * L) / (1 - (V)/(v))` =
`-(m*L)/(M + m) = -(3.63 kg * 2.50 m)/(198 kg + 3.63 kg) = -0.045 m`

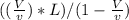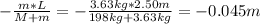
The minus sign means the displacement of the platform is in opposite direction to the displacement of the ball.