Question

Consider the sequence below.

-4, -1, 2, 5, . . .

What is the 10th term of the sequence?

Answer 1

35, because the intervals are +3,

3*10 = 30
Therefore,
5+30= 35

Answer 2

Answer: 23

Explanation: First of all, let's make sure we have an arithmetic sequence. An arithmetic sequence is a sequence that has a common difference which is the number repeatedly added or subtracted to reach the next term.

To get from -4 to -1, we're adding 3.

To get from -1 to 2, we're adding 3.

To get from 2 to 5, we're adding 3.

So we know that this is an arithmetic sequence because it has a common difference or the number that is repeatedly added which is 3.

Now, we want to determine the 10th term in this sequence.

There are 2 ways that you can determine the 10th term. You can keep on adding 3 until you get to the 10th term or you can use the explicit formula. I will show you the explicit formula which is shown below.

`^(a)n = ^(a)1(n - 1)d`

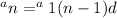
Now we want to determine what the 10th term is so we're trying to determine
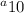`^(a)10`. Now, we know what
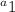`^(a)1` is because it's our first term or -4. Now, n will be the number of terms we're solving for or 10. Lastly, we have the d which represents the common difference which is 3.

So plugging into the formula, we have
`^(a)10 = -4 +(10 -1)(3)`.

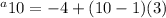Now, make sure we apply order of operations because this is where many students make mistakes.

(10 -1) is going to be 9. Then we want to make sure we multiply before we add so 9 x 3 is going to be 27 and then -4 + 27 is 23.

So the 10th term in this sequence is 23.