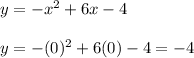Answer:
1. Axis of symmetry: x = 3
2. Vertex: (3,5)
3. Solution of the equation:

Step-by-step explanation:
1. Equation:
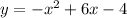
2. Axis of symmetry:
That is the equation of a parabola, whose standard form is:

Where:
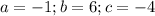
The axis of symmetry is the vertical line with equation:

Substitute
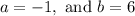
![x=-6/[(2)(-1)]=-6/(-2)=3](https://img.qammunity.org/2021/formulas/mathematics/middle-school/mryc77bh5f74iuhemjpsobrov52hvlpf0b.png)
Thus, the axis of symmetry is:
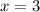
3. Vertex
The x-coordinate of the vertex is equal to the axys of symmetry, i.e x = 3.
To find the y-xoordinate, substitute this value of x into the equation for y:
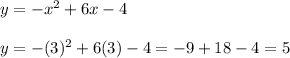
Therefore, the vertex is (3, 5)
4. Find the x-intercepts
The x-intercepts are the roots of the equation, which are the points wher y = 0.
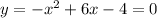
Use the quadratic equation:
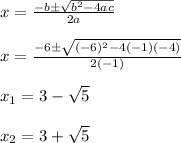
5. Find the y-intercept
The y-intercet is the value of y when x=0: