Answer:
The first choice,
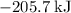 .
.
Step-by-step explanation:
Let the three reactions, where the enthalpy change were known, be called (1), (2), and (3).
The goal is to find the enthalpy change of the fourth equation. Assume that this equation can be written as
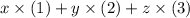 for some
for some
 ,
,
 , and
, and
 (might not be whole numbers or take positive values.) Then, by Hess's Law, the enthalpy change of that reaction would be
(might not be whole numbers or take positive values.) Then, by Hess's Law, the enthalpy change of that reaction would be
 .
.
To find these
 ,
,
 , and
, and
 , consider: what combination of reaction (1), (2), and (3) would give the fourth reaction?
, consider: what combination of reaction (1), (2), and (3) would give the fourth reaction?
Imagine that the coefficients are positive for all the reactants, and negative for all the products.
For example: in (1),
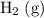 has a coefficient of
has a coefficient of
 . However, since it is on the the product side of (1), its value should be
. However, since it is on the the product side of (1), its value should be
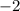 . Also, in (3)
. Also, in (3)
Since there is no
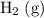 in the desired equation, the value of
in the desired equation, the value of
 ,
,
 , and
, and
 should ensure that
should ensure that
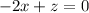 .
.
Another example:
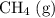 is on the reactant side of the first reaction. Its coefficient in the equation is
is on the reactant side of the first reaction. Its coefficient in the equation is
 , so that corresponds to
, so that corresponds to
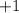 . Since
. Since
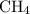 is neither in (2) nor in (3), the value of
is neither in (2) nor in (3), the value of
In the desired equation,
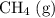 is on the reactant side with a coefficient of
is on the reactant side with a coefficient of
 . As a result, the value of
. As a result, the value of
 ,
,
 , and
, and
 should ensure that
should ensure that
 .
.
One such equation can be found for each species in the reactions.
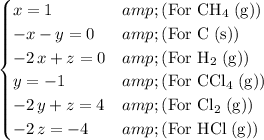 .
.
Solve this system of equations for
 ,
,
 , and
, and
 (this approach works only if at least one solution exists.) In this case,
(this approach works only if at least one solution exists.) In this case,
 .
.
Calculate the enthalpy change of the desired reaction:
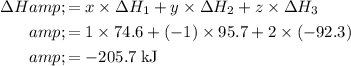 .
.