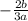Question

12abx square - (9a square - 8b square)x - 6ab =0

Answer 1

The value of x is
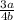`(3a)/(4b)` and
`-(2b)/(3a)`

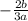
Step-by-step explanation:

The expression is
`12abx^(2) -(9a^(2) -8b^(2) )x-6ab=0`

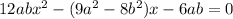
Multiplying the term x withing the bracket, we get,

`12abx^(2) -9a^(2) x+8b^(2) x-6ab=0`

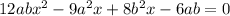
Grouping the terms, we have,

`(12abx^(2) -9a^(2) x)+(8b^(2) x-6ab)=0`

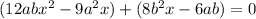
Taking out the common terms in each bracket, we get,

`3ax(4bx -3a)+2b(4bx-3a)=0`

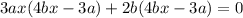
Simplifying, we get,

`(3ax+2b)(4bx -3a)=0`

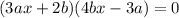
Equating each term to zero, we get,

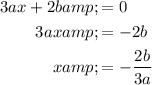`\begin{aligned}3 a x+2 b &=0 \\3 a x &=-2 b \\x &=-(2 b)/(3 a)\end{aligned}` and
`\begin{aligned}4 b x-3 a &=0 \\4 b x &=3 a \\x &=(3 a)/(4 b)\end{aligned}`

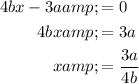
Hence, the values of x is
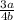`(3a)/(4b)` and
`-(2b)/(3a)`