Question

A chocolate factory produces mints that weigh 10 grams apiece. The standard deviation of the weight of a box of 10 mints is 3 grams. You buy a box of mints that weighs 95 grams. What is your confidence that the box you bought did not come from the factory?

90%
95%
10%
5%

Answer 1

The confidence that the box you bought did not come from the factory is 90 %.

Explanation:

Since we have given that

Population Mean weight (\mu)= 10 grams a piece

Standard deviation of the weight of a box = 3 grams

Number of mints = 10

We need to buy a box of mints that weighs 95 grams.

Sample mean is given by

x =
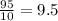`(95)/(10)=9.5` grams .

First we find out the standard error which is given by

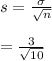`s=(\sigma)/(√(n))\\\\=(3)/(√(10))\\\\`= 0.94868

Since it is normal distribution, so, we will find z-score.

`z=(x-\mu)/(s)\\\\z=(9.5-10)/(0.94868)\\\\z=-0.527\\\\`

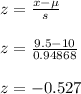
z = - 0.53

The area to the left of a z-score of -0.53 = 0.29805.

So, it may be 90% or 95 % confidence.

For 95% confidence level,

`\alpha=(1-0.95)/(2)=0.025`

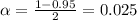
Similarly,

For 90% confidence level,

`\alpha=(1-0.90)/(2)=0.05`

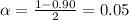
The value is much smaller than 0.05.

So, we will get 90% confidence and the critical value = 1.645

Margin of error is given by

(Standard deviation)
`*` (critical\ value) = 0.94868
`*` 1.645

=1.56

So, confidence interval will be

(10-1.56,10+1.56)

=(8.44,11.56)