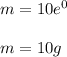Question

A colony of bacteria is growing at a rate of 0.2 times its mass. Here time is measured in hours and mass in grams. The mass of the bacteria is growing at a rate of 4 grams per hour after 3 hours.

Write down the differential equation the mass of the bacteria, m, satisfies: ′= .2m
Find the general solution of this equation. Use A as a constant of integration.
() = Ae^(.2t)
Which particular solution matches the additional information? () =
What was the mass of the bacteria at time =0? mass =

Answer 1

• Question 1:
  `dm/dt=0.2m`

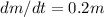
• Question 2:
  `m=Ae^((0.2t))`

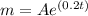
• Question 3:
  `m=10e^((0.2t))`

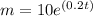
• Question 4:
  `m=10g`

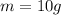
Step-by-step explanation:

Question 1: Write down the differential equation the mass of the bacteria, m, satisfies: m′= .2m

a) By definition:
`m'=dm/dt`

b) Given:
`rate=0.2m`

c) By substitution:
`dm/dt=0.2m`

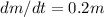
Question 2: Find the general solution of this equation. Use A as a constant of integration.

a) Separate variables

`dm/m=0.2dt`

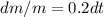
b) Integrate

`\int dm/m=\int 0.2dt`

`ln(m)=0.2t+C`

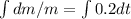
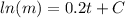
c) Antilogarithm

`m=e^(0.2t+C)`

`m=e^(0.2t)\cdot e^C`

`e^C=A\\\\m=Ae^((0.2t))`

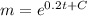
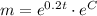
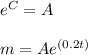
Question 3. Which particular solution matches the additional information?

Use the measured rate of 4 grams per hour after 3 hours

`t=3hours,dm/dt=4g/h`

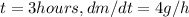
First, find the mass at t = 3 hours

`dm/dt=0.2m\\\\4=0.2m\\\\m=4/0.2\\\\m=20g`

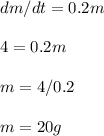
Now substitute in the general solution of the differential equation, to find A:

`m=Ae^((0.2t))\\\\20=Ae^((0.2* 3))\\\\A=20/e^((0.6))\\\\A=10.976`

Round A to 1 significant figure:

• A = 10.

Particular solution:

`m=10e^((0.2t))`

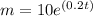
Question 4. What was the mass of the bacteria at time =0?

Substitute t = 0 in the equation of the particular solution:

`m=10e^(0)\\\\m=10g`